Developing an Intuition for Combinatorics: Permutations and Combinations

Understanding combinatorics in a few simple ways

Combinatorics was one of the most difficult concepts for me to understand when I first studied probability and statistics.

On the surface, the idea of combinations is simple. Some examples include:

• your outfit (ie. Which shirt should be paired with which pants?)

• phone passcode

• food toppings

However, suppose I asked you:

• “How many different outfits can you make?”

• “How many different passcodes are possible on your phone?”

• “How many different combinations of toppings can you order?”

Credit: NintendoLife

You may have a bit more of a difficult time answering these questions.

While the idea of combinations is simple, counting them can be more challenging.

But fear not because after reading this article, you’ll develop a better understanding of how to solve combinatorial problems.

What is Combinatorics?

Before we get our hands dirty with the math, let’s first understand what combinatorics is.

From the earlier questions, you may have already guessed it has something to do with counting the number of arrangements (or combinations) of things such as items, numbers, and people.

Combinatorics is the mathematical study of counting and arranging items.

We all have a fundamental understanding of counting and arranging, regardless of our social, academic, and professional backgrounds.

If I asked you to count the number of apples in the picture, you’d tell me there are 3.

Credit: Suzy Hazelwood

But if I ask you:

From a standard playing card deck, what is the number of possible arrangements of the deck?

Credit: Nhu Tran

This can be much more challenging because you’ll need to have prior knowledge of playing cards such as:

• What is a standard playing card deck?

• How many cards are in it?

• What are the cards in it? (ie. King of Spades, 1 of Hearts, etc.)

• Are we including the Joker?

• Etc.

While some textbooks tell you that a standard playing card deck consists of 52 cards, they often assume you know a deck has 12 Club cards, 12 Heart cards, 12 Spades cards, and 12 Diamond cards with each group having cards from 1 to King.

Credit: UChicago

From the image, we can imagine some starting combinations to look like:

• King❤️, 7♠️, 8♦️, Queen♣️, Jack♦️, Ace❤️, Ace♠️, 9♦️, 3♣️, King♦️, …

• Ace❤️, Ace♠️, 9♦️, 3♣️, King♦️, 9♣️, 7♠️, 9♦️, 1♦️, Queen♠️, …

Obviously, these aren’t all the possible arrangements but finding the total number of arrangements this way would be too time-consuming and difficult.

And lastly, what if I asked you:

How many 6-digit passcodes can you make on your phone?

Credit: iStock

Some examples are:

• 194063

• 174592

• 110483

Again, this list isn’t exhaustive because it would be quite long.

But I’m trying to illustrate that counting can be more difficult than what we’re used to. Certain conditions such as the number of items, order, and repetitions can make our natural way of counting inefficient.

Fortunately, combinatorics can help us find these solutions much more efficiently.

The Basics

Let’s start with a relatively simple and relatable example.

Suppose you just bought a new phone and you’re asked to create a new passcode.

While some phones allow you to use other characters such as letters, for simplicity, let’s only use digits 0 to 9 (ie. 0, 1, 2, 3, …, 8, 9).

Credit: Make Use Of

Normally, phones ask you to create a passcode with at least 4 digits.

Before answering the following:

How many different 4-digit passcodes are there?

Let’s first ask:

How many different 1-digit passcodes are there?

This seems simple enough because we only have the digits 0 to 9. You can count it yourself and see that there is a total of 10 unique 1-digit passcodes (0, 1, 2, 3, … , 9).

Now, let’s then see how many 2-digit passcodes there are.

We know that the lowest two-digit combination is 00 and the highest is 99. So from 00 to 99, there is a total of 100 different 2-digit combinations.

How about 3-digit passcodes?

If you guessed 1000, you are correct! From 000 to 999, we have a total of 1,000 different 3-digit passcodes.

Hopefully, you see the pattern now to finally answer the original question:

How many different 4-digit passcodes are there?

From 0000 (terrible passcode) to 9999 (just as terrible), there are 10,000 different 4-digit passcodes!

With 10,000 possible passcodes, it can be difficult for others to access your phone. This is why programs and services always ask you to create a long and difficult password. The longer the password, the harder it is to guess the right one.

What if I asked:

How many different n-digit passcodes are there, where n is a whole number greater than 0?

While we know that it’s 10ⁿ different combinations, let’s look at it from a more mathematical approach.

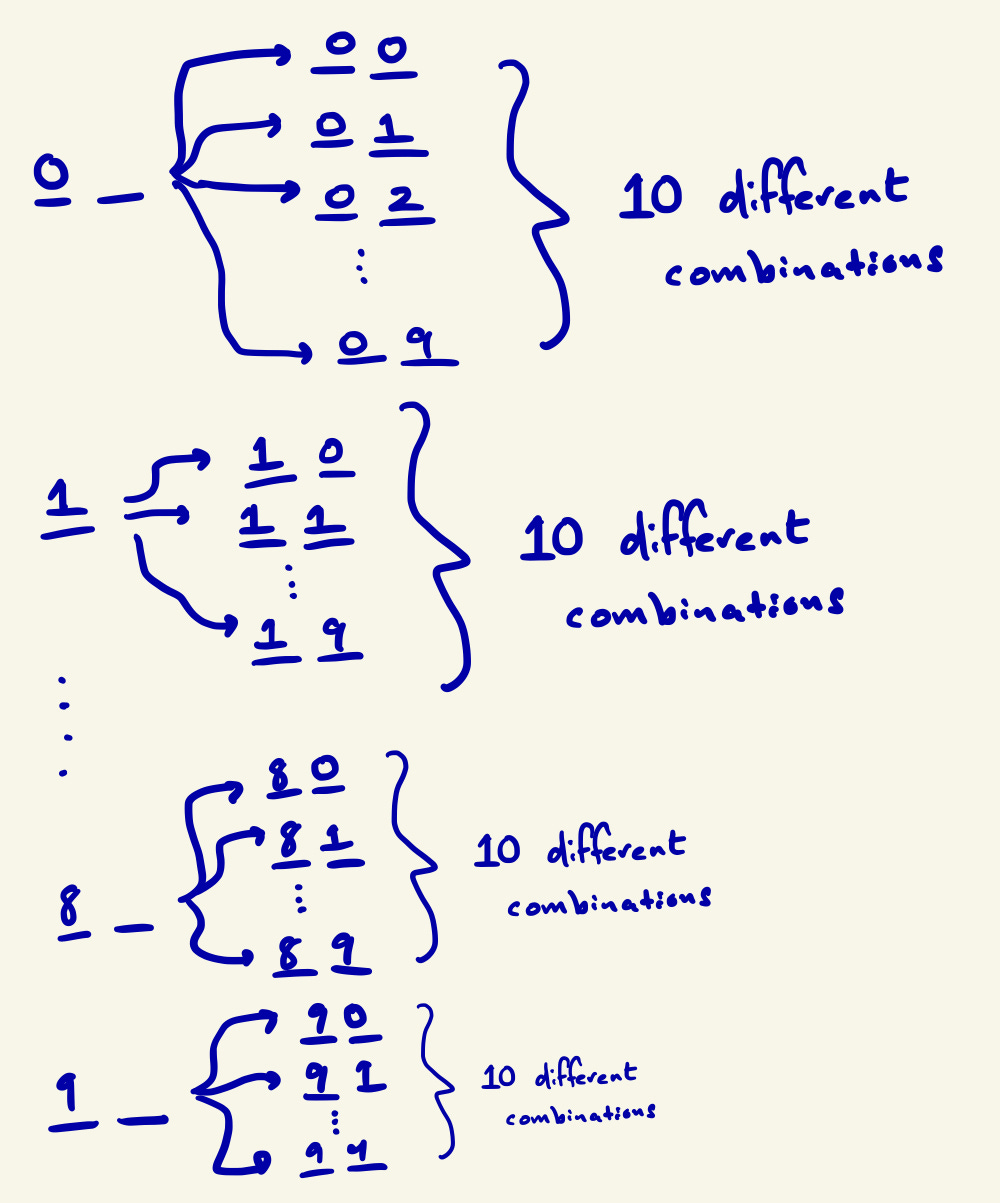
Let’s take a look at 1-digit combinations. As we discussed earlier, the values are numbers 0, 1, 2, 3, …, 8, 9, which makes a total of 10 different combinations.

For 2-digit combinations:

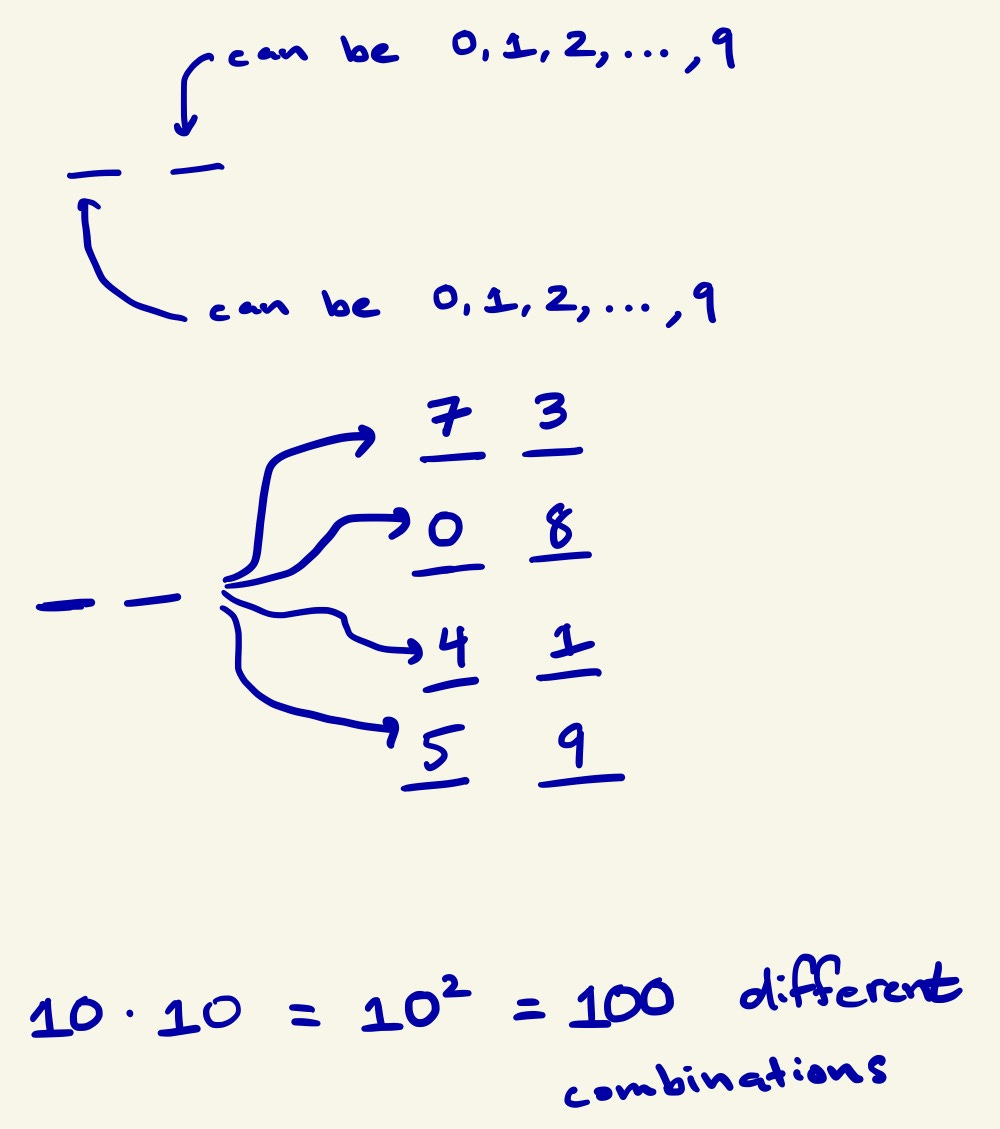
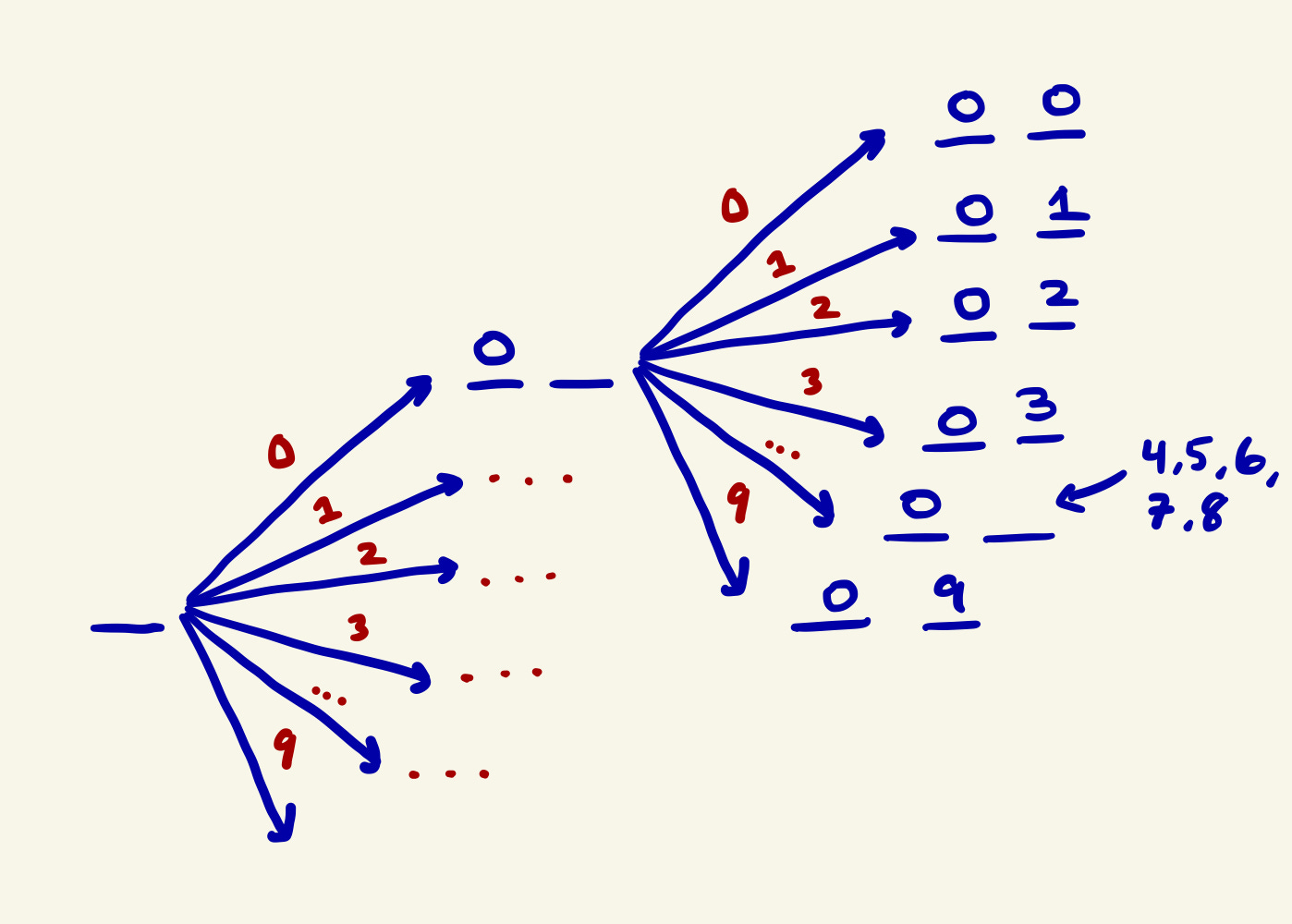
You’re probably wondering where 10 x 10 = 10² = 100 came from. Here’s a diagram to show you the different combinations.

Suppose we have the following: _ _

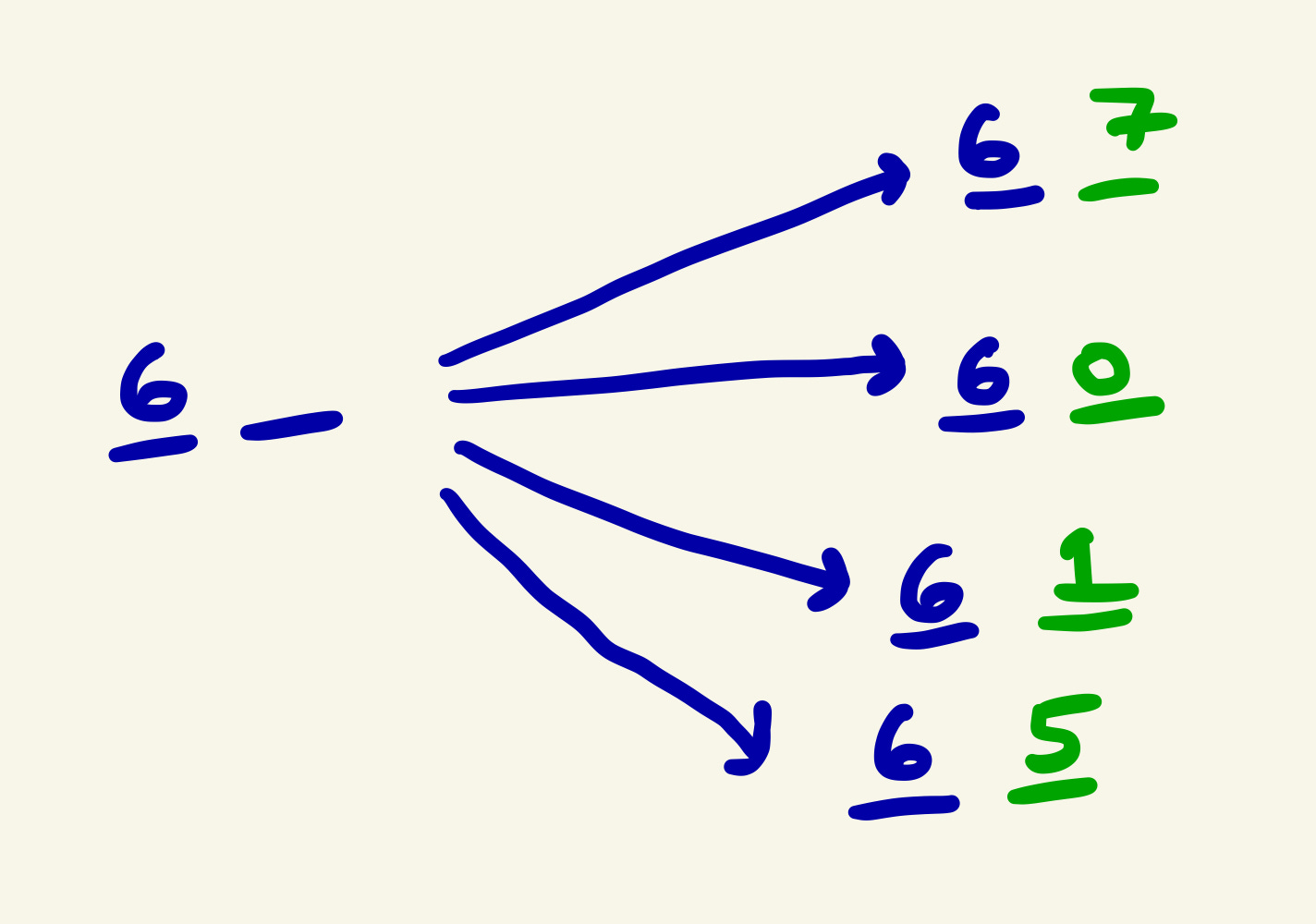
Let’s select a random number (from 0 to 9) for the first digit (the tens digit). Let’s say: 6

So now, we have: 6_

The ones-digit that follows 6 can be any number from 0 to 9 such as 67, 60, 61, and 65. There are a total of 10 different combinations with 6 as a starting digit.

Just a few combinations starting with 6

However, the tens-digit can be any number from 0 to 9. That means that each digit also has 10 different combinations.

Another way to look at it is through a decision tree:

With the decision tree, you can see how each branch has 10 additional branches.*

Note: I don’t recommend using a decision tree for these types of problems because the decision tree becomes more complex as the number of combinations increases.

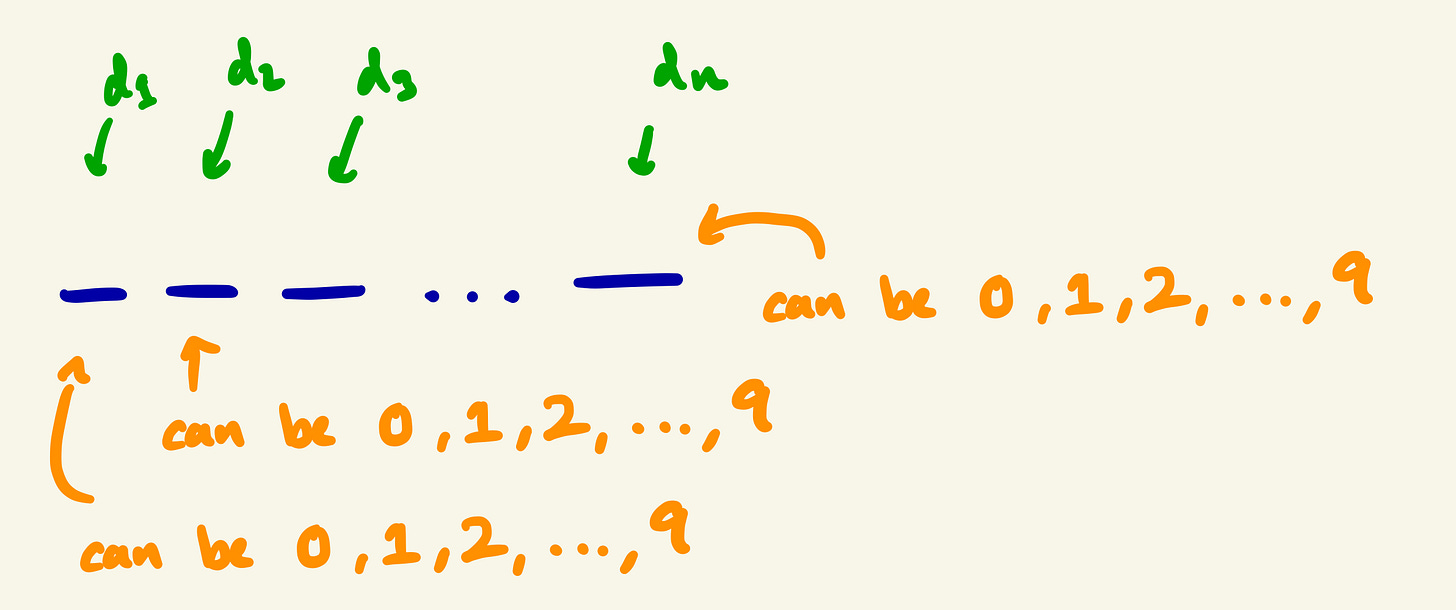
The main point that I want to illustrate is that we can break this down to a simple formula:

\(t_1 \times t_2 \times t_3 \times ... t_n = \text{total number of combinations / outcomes}\)

Note: t_i (where i can be 1 to n) represents the total number of choices for the i^th position.

So in the case of 1-digit, we only have:

\(t_1 = 10\)

Because there are only 10 choices for the 1^st (and only) position.

For 2-digits, we have:

\(t_1 \times t_2 = 10 \times 10 = 100\)

Since there are 10 choices for the 1^st position and 10 choices for the 2^nd position, there is a total of 100 combinations.

We can now generalize this for n-digits to look like this:

\(t_1 \times t_2 \times t_3 \times ... t_n = \text{total number of combinations / outcomes}\)

And that’s how we arrive at a total of 10ⁿ different combinations for n-digit passcodes.

Where d represents a selected digit from 0 to 9 (ie. d₁d₂ = 43, where d₁ = 4 and d₂ = 3).

Permutations

Now that we have a basic understanding and framework of combinations, let’s look at permutations.

Permutation has the following restrictions:

• Order matters (ie. ACD ≠ DCA)

• No repetition

Intuitively, we understand that order is important for some things.

In our passcode example, if a passcode is 4291, 4 must come first, followed by 2, then 9, and lastly 1. If you enter: 2914, this is a completely different passcode and is considered incorrect.

No repetition is another important restriction because there are moments when we can only use something once.

In our passcode example, we can use each number multiple times. Let’s suppose we have a passcode: 1451. This is a valid passcode code. Order matters but since 1 is used twice, it violates the no-repetition restriction. Therefore, it is not a permutation.

Another example, a bit more complex but important in the field of computational biology, is gene sequencing. From basic biology, we know that combinations and sequences of DNA nucleotides C, G, T, and A impact our health. A sequence such as CTGAGACT may cause cancer but another sequence of CTAGGACT may not.

Credit: Science Service

Now that we understand the importance of order and no repetition, let’s look at an example of permutation.

If you’re a fan of Blackpink, you may enjoy this example.

Suppose we have four chairs and four people: Jisoo, Jennie, Rosé, and Lisa.

How many different seating arrangements, or permutations, can we make from this group?

(Left to right) Jisoo, Jennie, Rosé, Lisa / Credit: YouTube

In the picture above, we have the following permutation:

• Jisoo, Jennie, Rosé, and Lisa

Other possible seating arrangements are:

• Jennie, Lisa, Rosé, and Jisoo

• Lisa, Jisoo, Jennie, and Rosé

But exactly, how many different permutations are there? Instead of writing out each arrangement and counting them, let’s use the method we learned earlier.

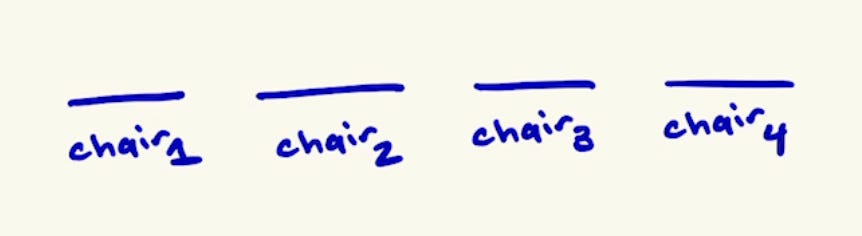
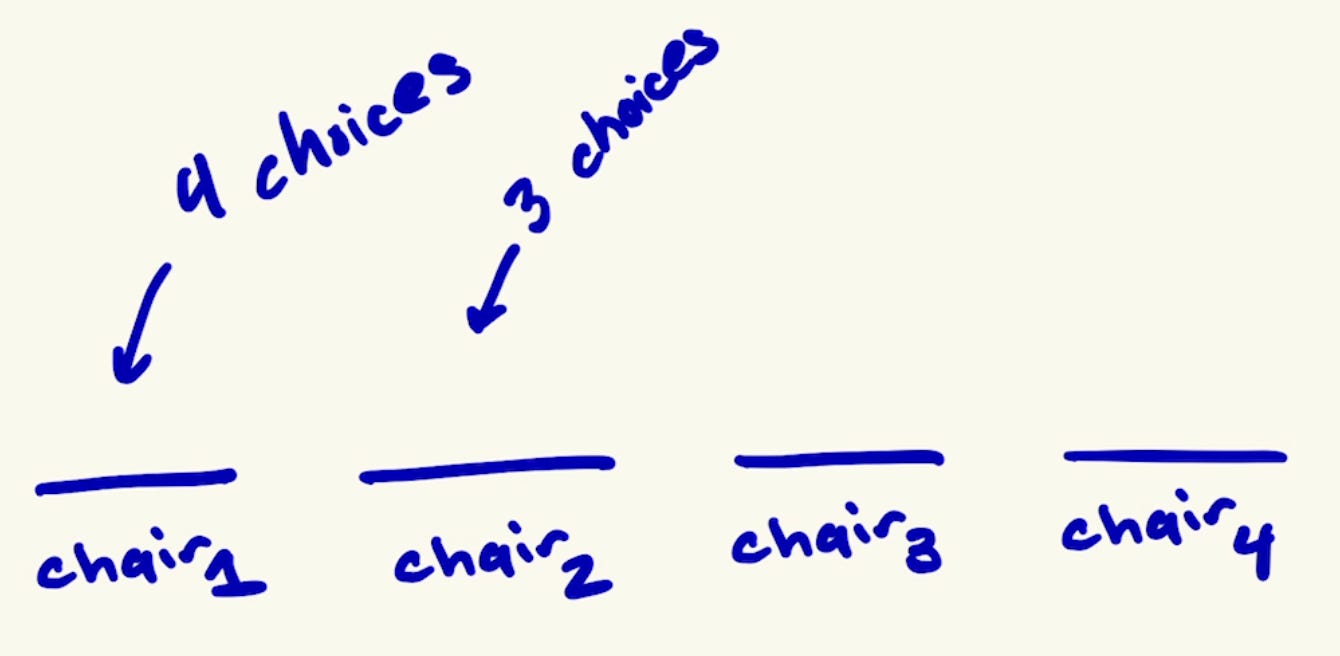
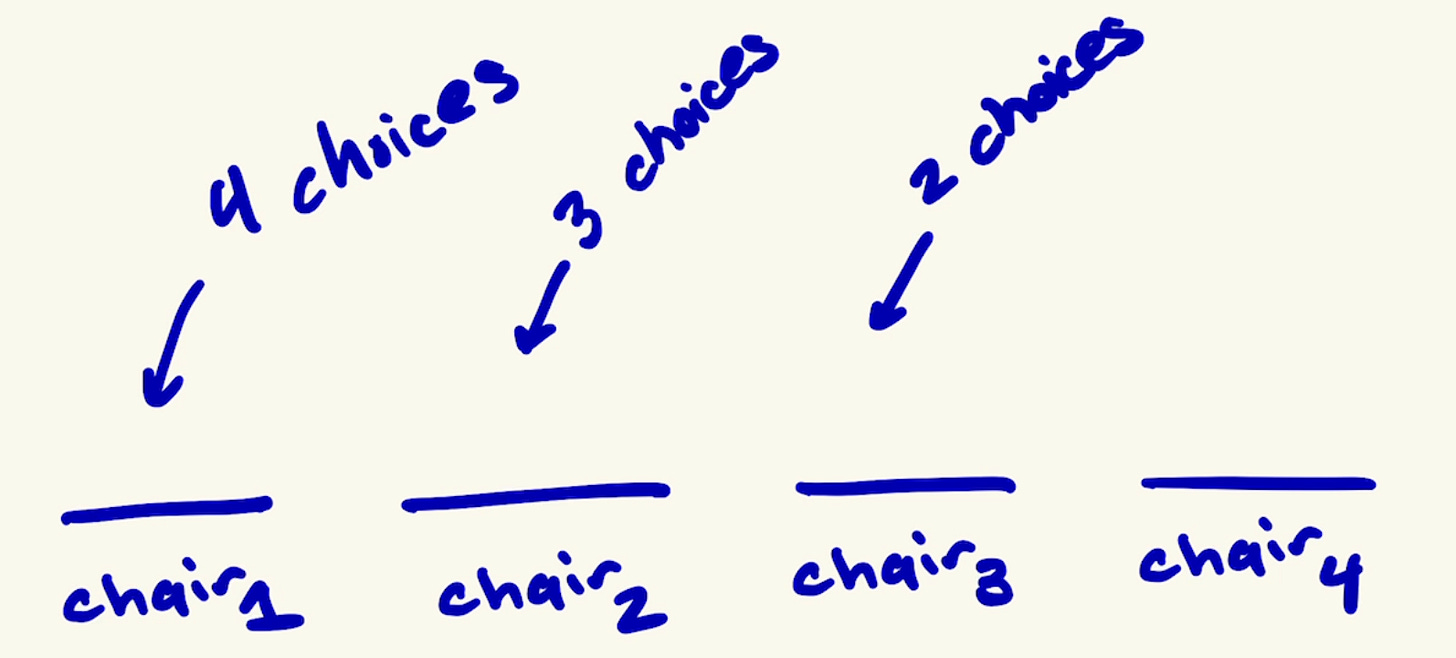
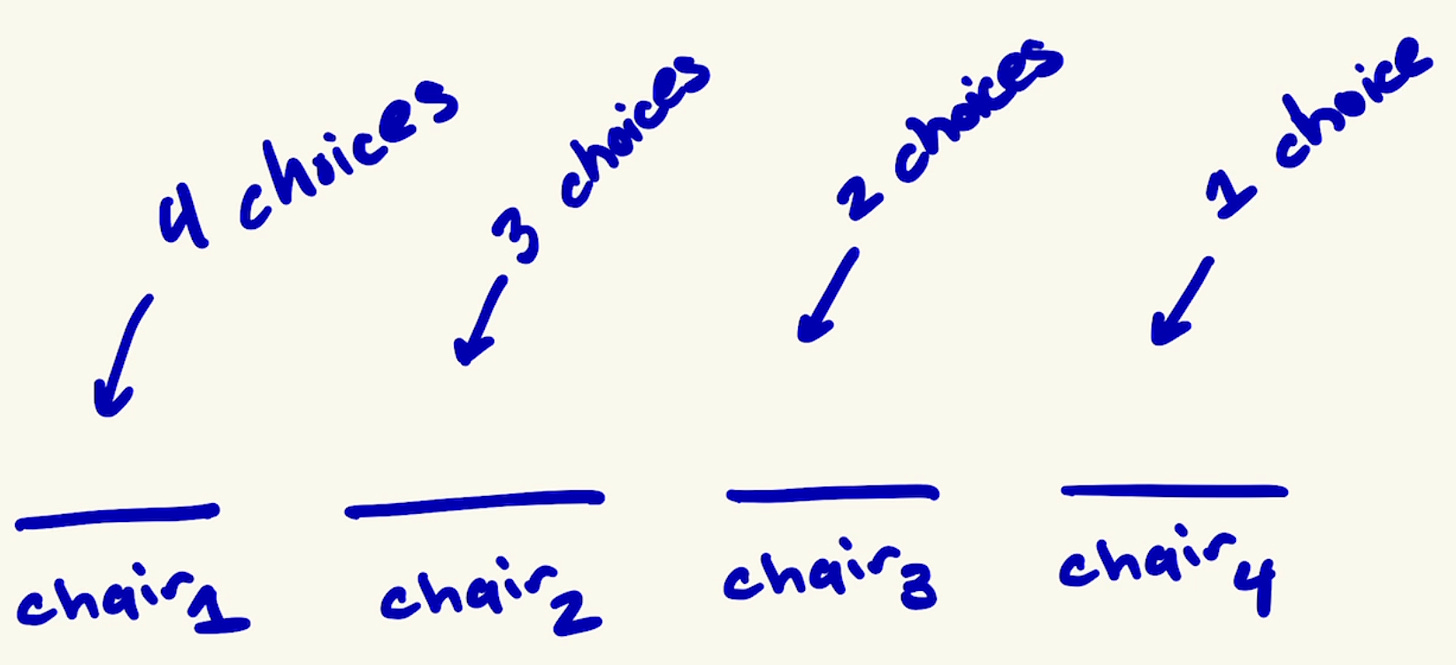
Suppose we have four empty chairs:

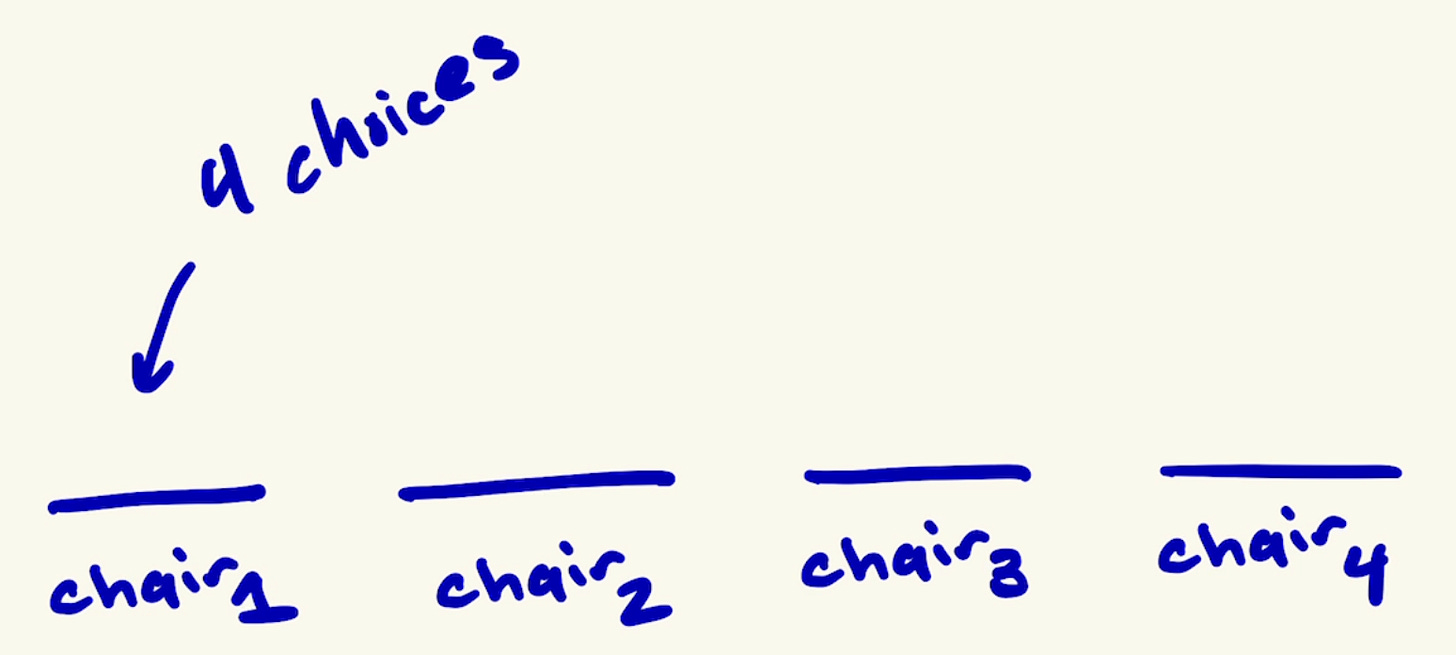
How many different ways can the first chair, chair₁, be assigned? Since no member has sat down yet, we have 4 different possibilities for who can sit on chair₁:

• Jisoo

• Jennie

• Rosé

• Lisa

Pick any one of the members to sit in chair₁.

Now that chair₁ is filled, we move on to chair₂.

However, unlike chair₁, where we had 4 people to choose from, now we only have 3 choices left. We cannot select the person we placed in chair₁ to sit in any other chair. It doesn’t make sense because they can’t be in two places.

Once we have selected someone for chair₂, we move on to chair₃ where we have 2 choices left.

I hope you’re starting to see the pattern.

For the last chair, chair₄, we only have 1 choice left.

Similar to the combination formula we learned earlier, we see there are:

\(4 {\times}3{\times}2{\times}1 = 24 \text{ different seating arrangements / total permutations}\)

We can also shorten this to:

\(4! = 4 {\times}3{\times}2{\times}1 = 24 \text{ different seating arrangements / total permutations}\)

“!” is short for “factorial”. This just means:

\(n! = n \times (n - 1) \times (n - 2) \times ... 2 \times 1\)

Important:

• n is a non-negative whole number (ie. 0, 1, 2, 3, …)

• 0! = 1

Here’s a tree diagram to illustrate the logic. Again, while drawing a tree diagram is a valid method to solve these problems, it’s inefficient, especially as the number of choices gets larger.

Let’s make this a bit more challenging.

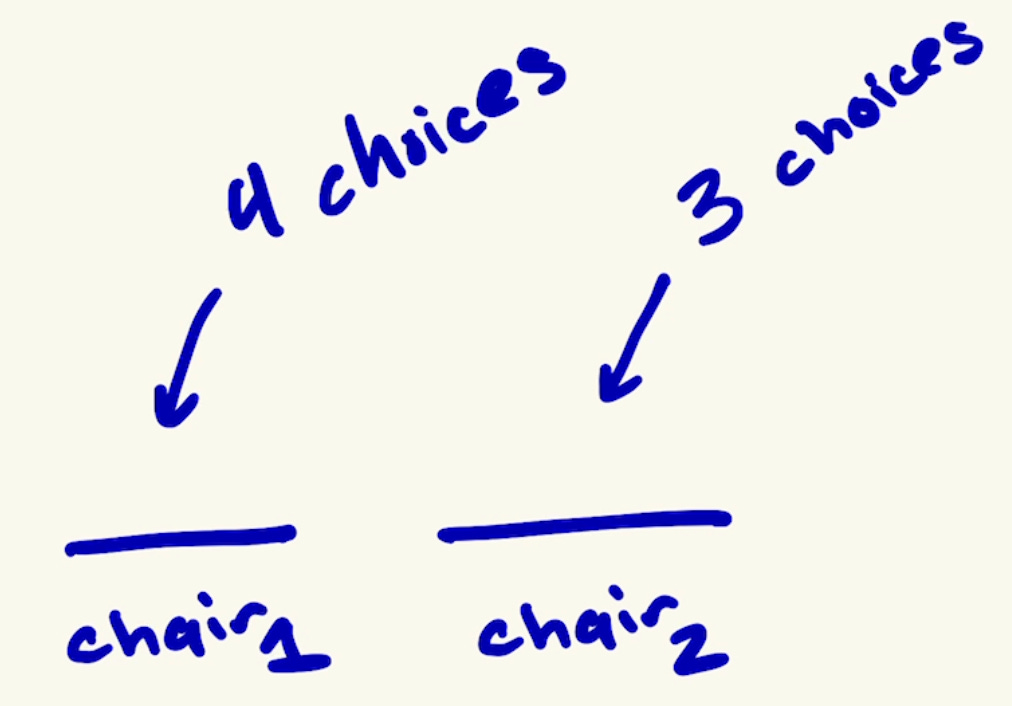
Suppose there are only 2 chairs and we still have 4 group members to choose from.

How many different seating arrangements are there?

We’ll apply the same logic as earlier but stop once chair₂ has been filled.

We see that there are a total of:

\(4 \times 3 = 12 \text { different seating arrangements for 2 chairs and 4 group members}\)

Doesn’t the above equation look like 4! has been cut short? We still have 4 x 3 without the 2 x 1. Well, this is actually what it looks like:

\(4 \times 3 = \frac{4 \times 3 \times 2 \times 1}{2 \times 1} = \frac{4!}{(4 - 2)!} = \frac{4!}{2!} = 12\)

In fact, we can generalize this equation into a formula:

\(\text{ total number of permutations for choosing r items from n items} = \frac{n!}{(n - r)!}\)

In math books, you may see:

\(\text{P(}n,r \text{)}= _n\text{P}_r = \frac{n!}{(n - r)!}\)

P, if it’s not obvious, stands for Permutation.

Let’s slow down and discuss what this formula means.

In the previous example, we are given 4 Blackpink members to choose from but there are only 2 seats, which means that we can only select 2 members to sit on them.

In this situation, n = 4 because we only have 4 choices (Blackpink members). However, we can only choose r = 2 of those 4 choices to fill in the 2 seats.

To better understand this, think of it like this:

We have n! total seating arrangements (permutations) but we have to remove (n - r)! arrangements. Think of dividing (n - r)! as removing the excess.

If we have 4 members but only 1 chair, then we have n = 4 and r = 1. This means that we have a total of:

\(\frac{4!}{(4 - 1)!} = \frac{4!}{3!} = 4 \text{ different seating arrangements}\)

This makes sense because if we only have 1 seat, there are 4 different permutations.

If there were 4 seats, then we’d have, as we saw earlier:

\(\frac{4!}{(4 - 4)!} = \frac{4!}{0!} = \frac{4!}{1} = 24 \text{ different seating arrangements}\)

Important

Before we move on, I must clarify a few things we discussed earlier.

Remember the passcode example?

I used the term “combination” because it’s a more colloquially used term and an easier way of introducing sequences. But we know that 151 and 511 are different passcodes. Therefore, we say that any sequence where order matters is a permutation.

Combinations

This idea is much simpler than permutation because order doesn’t matter.

Even though we were allowed to repeat selections in the earlier examples of combinations, this section deals with no repetition.

If we continue with our Blackpink example, these arrangements are identical:

• Jisoo, Lisa, Rosé, and Jenny = Rosé, Jisoo, Jenny, and Lisa = Lisa, Jenny, Rosé, and Jisoo

Suppose we return to the example where there are only 2 chairs.

For permutation:

• Lisa, Rosé ≠ Rosé, Lisa

For combination:

• Lisa, Rosé = Rosé, Lisa

So how can we mathematically remove the duplicates if order doesn’t matter?

It’s simple, we divide by r!

\(\text{total combinations of n choose r} = \frac{n!}{(n - r)!} \times \frac{1}{r!} = \frac{n!}{(n - r)!r!}\)

But why are we dividing by r!? In this context, r! means the number of arrangements we can make from our choices. If we pick 3 members (r = 3), then we can arrange those 3 members in 3! ways amongst themselves. Since, in this context, order doesn’t matter, we must remove 3! from our combination count.

In math books, you may see:

\(\text{C(}n,r \text{)}= _n\text{C}_r = \frac{n!}{(n-r)!r!}\)

So if we have n = 4 members and r = 3 chairs, which means we can only select 3 of the 4 members to sit, then we have:

\(\text{C(}4,2 \text{)} = \frac{4!}{(4-3)!3!} = \frac{4!}{1!3!} = 4 \text{ different seating arrangments}\)

To drive this point further, suppose that Rosé, Lisa, and Jisoo are selected.

According to permutation, the orders:

• Rosé, Lisa, Jisoo

• Rosé, Jisoo, Lisa

• Jisoo, Lisa, Rosé

• Jisoo, Rosé, Lisa

• Lisa, Jisoo, Rosé

• Lisa, Rosé, Jisoo

are 3! = 6 different sequences.

But in the context of combination, they’re indistinguishable. 3! is the number of ways we can arrange Lisa, Rosé, and Jisoo’s seating order. Since 3! arrangments are identical, we have to divide by 3! to remove the duplicates from our count.

Summary

Combinatorics provides us with efficient methods of counting arrangements of items without having to draw them all out.

In this article, we learned and developed an intuition for the basic, yet powerful, concepts of permutations and combination.

Remember, if:

• Order does matter and you can repeat, then use the following permutation equation:

\(t_1 \times t_2 \times t_3 \times ... t_n = \text{total number of permutations / outcomes}\)

• Order does matter and you can’t repeat, use the permutation equation:

\(\text{P(}n,r \text{)}= _n\text{P}_r = \frac{n!}{(n - r)!}\)

• Order doesn’t matter and you can’t repeat, use the combination equation:

\(\text{C(}n,r \text{)}= _n\text{C}_r = \frac{n!}{(n-r)!r!}\)